Kontūras (matematika)
| |
Šį puslapį ar jo dalį reikia sutvarkyti pagal Vikipedijos standartus. Jei galite, sutvarkykite. |
 Kitos reikšmės – Kontūras (bangos).
Kitos reikšmės – Kontūras (bangos).
Geometrijoje kreivių šeimos kontūras plokštumoje yra kreivė, kuri tam tikru momentu yra liestinė kiekvienam kreivių šeimos nariui ir šie lietimo taškai kartu sudaro visą kontūrą.[1] Klasikiniu požiūriu taškas ant kontūro gali būti laikomas dviejų be galo mažų gretimų kreivių sankirta, o tai reiškia gretimų kreivių susikirtimų ribą. Šią idėją galima apibendrinti į paviršiaus kontūrą erdvėje ir taip toliau į aukštesnius matmenis.
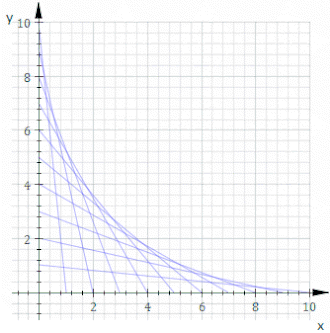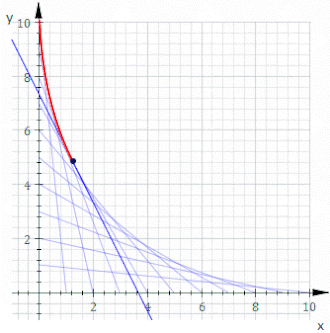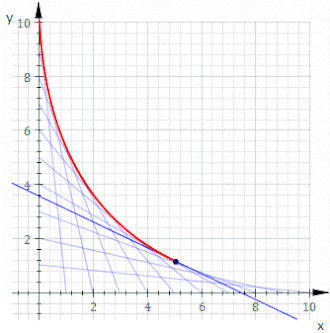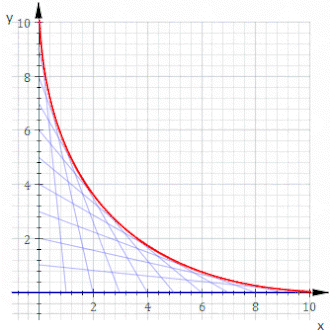
Norint turėti kontūrą, būtina, kad atskiri kreivių šeimos nariai būtų diferencijuojamos kreivės, nes kitaip liestinės sąvoka netaikoma, ir turi vykti sklandus perėjimas pro kreivių šeimos narius. Tačiau šių sąlygų nepakanka – tam tikra kreivių šeima kontūro gali ir neturėti. Paprastas to pavyzdys yra besiplečiančio spindulio koncentrinių apskritimų šeima.
Šaltiniai
redaguoti- ↑ „Envelope | Curves, Surfaces & Geometry“. Encyclopedia Britannica. Nuoroda tikrinta 2024-02-02.