Trikampio nelygybė

Šiam straipsniui ar jo daliai trūksta išnašų į šaltinius. Jūs galite padėti Vikipedijai pridėdami tinkamas išnašas su šaltiniais.

Trikampio nelygybė teigia, kad bet kokio trikampio bet kurių dviejų kraštinių ilgių suma yra nemažesnė už trečios kraštinės ilgį. Euklido geometrijoje ir kai kuriose kitose geometrijose tai yra teorema. Euklido geometrijoje dviejų kraštinių ilgių suma yra lygi trečiosios kraštinės ilgiui tada ir tik tada, kai trikampis turi vieną 180° kampą ir du 0° kampus, kaip parodyta apatiniame dešinėje esančio paveikslėlio pavyzdyje.

Du trikampio nelygybės pavyzdžiai. Viršutinis brėžinys yra pavyzdys, kai galima pritaikyti griežtą nelygybę, nes visi kampai yra mažesni už 180°. Apatiniame pavyzdyje dviejų kraštinių suma yra lygi trečiajai kraštinei.

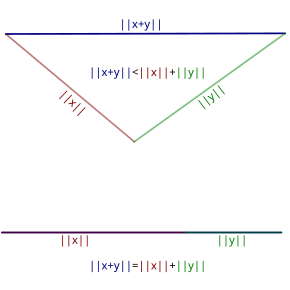
Normuotoje vektorinėje erdvėje V, trikampio nelygybė yra

$\displaystyle \|x+y\|\leq \|x\|+\|y\|\quad \forall \,x,y\in V$

t. y. dviejų vektorių sumos norma yra nedidesnė už tų pačių dviejų vektorių normų sumą.

Realiųjų skaičių tiesė yra normuota vektorių erdvė, kurioje norma yra modulis. Taigi, tirkampio nelygybė teigia, kad bet kuriems realiesiems skaičiams x ir y galioja nelygybė

$|x+y|\leq |x|+|y|.\,$

Iš atvirkštinės trikampio nelygybės išeina, kad bet kuriems realiesiems skaičiams x ir y galioja ir nelygybė

$|x-y|\geq {\bigg |}|x|-|y|{\bigg |}.$