Taisyklingas ikosaedras
| Taisyklingas ikosahedras | |
|---|---|
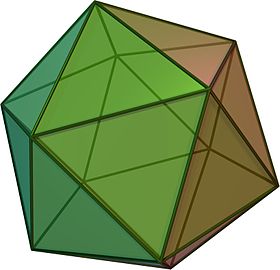 (Čia spustelėjus, suksis) | |
| Tipas | Platono kūnas |
| Elementai | F = 20, E = 30 V = 12 (χ = 2) |
| Sienos pagal puses | 20{3} |
| Konvėjaus užrašas | I sT |
| Šlėfli simbolis | {3,5} |
| s{3,4} sr{3,3} or | |
| Vithofo simbolis | 5 | 2 3 |
| Kokseterio diagrama | |
| Simetrija | Ih, H3, [5,3], (*532) |
| Sukinio grupė | I, [5,3]+, (532) |
| Indeksai | U22, C25, W4 |
| Savybės | taisyklingas iškilas deltaedras |
| Dvisienis kampas | 138.189685° = arccos(-√5/3) |
 3.3.3.3.3 (Viršūnės planas) |
 Taisyklingas dodekaedras (dualus briaunainis) |
 Išklotinė | |
Geometrijoje taisyklingas ikosaedras – iškilasis briaunainis, turintis 20 sienų, 30 briaunų ir 12 viršūnių. Tai vienas penkių Platono kūnų.
Jo penkios lygiakraščių trikampių sienos susieina kiekvienoje viršūnėje. Šio briaunainio Schläfli simbolis yra {3,5}, arba kartais jis žymimas pagal viršūnės planą – 3.3.3.3.3 arba 35. Ši figūra yra duali su taisyklingu dodekaedru, kuris žymimas simboliu {5,3}, tai yra, turi tris taisyklingų penkiakampių sienas, sueinančias kiekvienoje viršūnėje.
Taisyklingas ikosaedras yra penkiakampė bipiramidė ir kartu biaugmentinė penkiakampė antiprizmė bet kuria iš šešių krypčių.
Pavadinimas yra kilęs iš graikų kalbos είκοσι (eíkosi) 'dvidešimt' ir εδρα (hédra) 'siena'. Euklidas sukonstravo taisyklingąjį ikosaedrą, gaudamas iš pradžių du penkiakampius, priklausančius dviem lygiagrečioms plokštumoms – iš dešimties viršūnių ir po to pridėdamas dvi likusias priešingas viršūnes.[1] Papas Aleksandrietis įrodė, kad taisyklingojo ikosaedro viršūnės po tris priklauso keturioms lygiagrečioms plokštumoms, sudarant kiekvienoje iš jų taisyklingąjį trikampį. Prie kiekvienos šio ikoseadro viršūnės esančių plokščiųjų kampų suma lygi 300°.[2]
Išnašos redaguoti
- ↑ Euklid's Elements. Book XIII. Proposition 16
- ↑ Vaidotas Mockus. Geometrijos žinynas moksleiviams. – Šiauliai: Šiaulių pedagoginis institutas, 1996. – 141 p. ISBN 9986-38-010-3
